Погрузка и разгрузка поездов

TBD

Эта статья писалась в те времена, когда аффтар был маленький. Стиль изложения и качество видео оставляет желать лучшего. Но в будущем есть планы переписать и переснять всё. Пока страдайте тем, что есть.

Для быстрой погрузки и разгрузки предметов всегда используйте железный сундук Iron chest или стальной сундук Steel chest между грузовым вагоном Cargo wagon и конвейерами Belts транспортирующими предметы. При погрузке и разгрузке жидкостей используйте резервуар Storage tank между помпой Pump и трубами Pipe транспортирующими жидкости. В таком случае, сундуки и резервуары будут выполнять роль cache при перемещении предметов и жидкостей между поездами.

Вы можете разместить до 6 манипуляторов с каждой стороны грузового вагона, максимум 12 манипуляторов с обеих сторон. Использование твёрдотопливных манипуляторов Burner inserter крайне не эффективно и может использоваться только при погрузке и разгрузке топлива. Обычные жёлтые манипуляторы Inserter можно использовать если подающие предметы конвейеры не наполняются полностью, например для предметов, требующих много времени на производство. Длинные манипуляторы Long-handed inserter не очень удобны, кроме погрузки артиллерийских снарядов Artillery shell в железнодорожное артиллерийское орудие Artillery wagon, чтобы увеличить количество промежуточных сундуков из-за малого количества предметов в стопке. При разгрузке стоит использовать только пакетные манипуляторы Stack inserter, в крайнем случае быстрые манипуляторы Fast inserter. Должны быть завершены все исследования бонусов вместимости манипулятора Inserter capacity bonus.

Вы также можете разместить до трёх помп с каждой стороны вагона-цистерны Fluid wagon, всего 6 помп с обеих сторон. Но такое количество помп не целесообразно, две помпы на вагон-цистерну вполне достаточно.

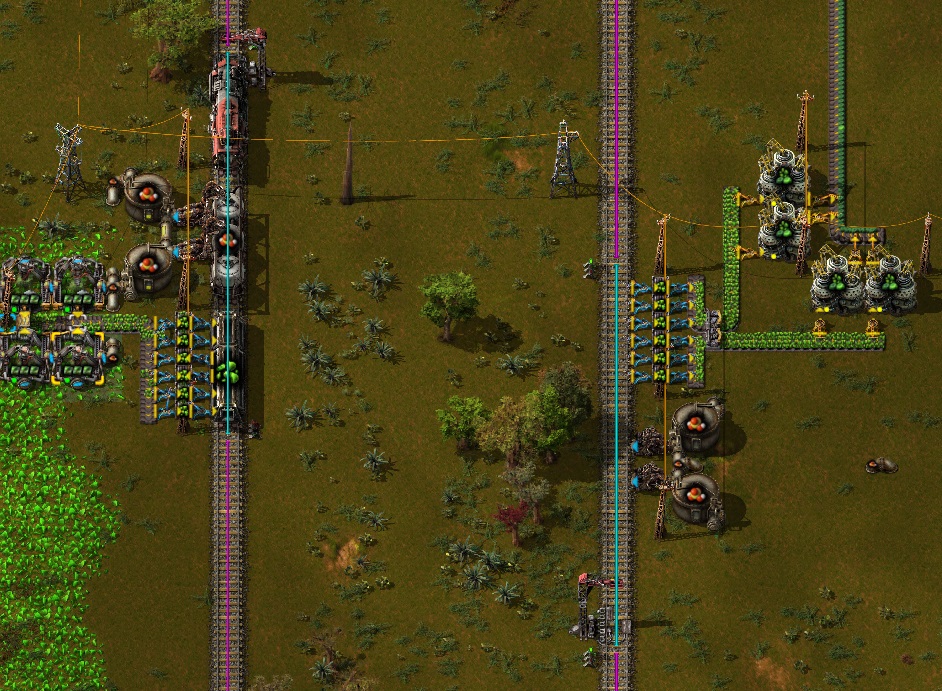
Разгрузка предметов

Согласно Factorio wiki 6 пакетных манипуляторов Stack inserter, пристыкованных с одной стороны грузового вагона, способны постоянно выгружать примерно 1.85 полных полос экспресс-конвейера Express transport belt, если каждый манипулятор будет выгружать на выделенную полосу (lane) конвейера. Это теоретически максимально возможная скорость разгрузки грузового вагона. Соответственно, если окружить 4-х вагонный поезд манипуляторами с обеих сторон, то общая выгрузка будет примерно 14.8 полных полос экспресс-конвейера (примерно 7.4 с каждой стороны поезда). Следующий чертёж демонстрирует как можно организовать такую выгрузку.

blueprint

0eNqlnW1uHUeSRbdi8DdlVFZ+ewG9iYEwkO0HNzEyJZDUoA3Dex/S0rifWlX0yTi/um1LeV/ciKrKjIi88fvNj+8/XT4+3N0/3fzw+83Pl8efHu4+Pt19uL/54SaV78d3l399fLg8Pn739PDu/vHjh4en7368vH96vLm9ufvpw/3jzQ//9fvN490v9+/evyzw9NvHy/PfvHu6/Pr8J+7f/fryT1+WePPXEm9elrj543mJ+58v/7r5If1x+7eLPLy7e3/1V/Y/3t7eXO6f7p7uLp9/xJ//8Nt/33/69cfLw/Oaf/3Nx2fcu1/++fTmzyVubz5+eLz7bOHvN88rzdlvb367+eFNH/OPlx/yHwvtf2fHwYrp+/r/a7bv6/Ov/vnu4fLT5z/SDjByAGN7BaMcYJQAxr5oR70i/d1P//Pm7v7x8vD0/F8O1s6vrL0frN2u1r5c3r/56Z+Xx8MfXb5e+GCp/lVUvfkSeQdL1X8v1Y+XGgsW10WL519r/3r5+e7Tr28u75//+MPdT28+fnh/+RvT+58I95fnyP/xw6eHl2ck5dvZ3h4ApS3wsPQjOlJa4GMsRlfaaQjMvw2BlJfJna+SO2/Tlg7JXX/w0ralxVhJ/NF7Xn1bZb5FbNgX31Cpr7+ixpVXCjJlBEDGKyCHlkxnSSUg++a+TPX4ydiTWxZ5Yd/dF68iEPlZRa7e5XeVWRL8sFby6thbbPGCFu+OHhZNI7A3KCfhPwNrnTxKeYvtDhCzOcUWRzGR98CO4JiDHNsRIMfnElscPXS5BrYbJ1GVW2Cts6jqckPBImAENxTMcVPagB6RsgVtQPFRktwUIT+UXaKgr1jJEZS8uGMpRaIwr9cISlllrAW2eP3fIDsCkTtiBjIcSEYg0227d5R+2BwIsqQmt6vMyBK5P0aOr9nt9JlPigPJxx/BGtwRZ/IGqcEd8Y4WlztixvpwICxII1vl/difbQusdRIbLbgzRu5re2xxFHgtB7bd+ZCD4M4YRVerscVRVLXIVvksqnpgrbOoGnLLyiJgBresyHE9uiFGnutJMoQewG43xOjb2LNEQd7udkOMdiy9ShTml1COuK7a0uXmnnl/SBTm/SkZQ7aMyKb4CmRDIMmdhhJ5v4zApvil8nAKcmhJdiAbsqQ4uphPqjsNMUuaOzwyx3dnCXO8PAYzn0x3rkOWzM2BIMdPWSZKx7usuceOXgkV1LM7FaFgnSVwkjljo8YOG4yNZvoLtpMS+O0+x1EZfEaaLrYTWkbgmJQOV5qxkwyKhOePdeD4cRIKL9SKjoXtpB3kNm/5uCVkDx4VIDVZnhVQiKfNbrDRWz1tVZ4WoDVNWpOYNXaPvTFrhtz+QtKmtIaRljZpDYu0FDpjt2VrQofsvmxNltawSEtFHYH6ZMZUhzLQizNFNtzlFZRjW7o6oHzL2LEtQ521qF+ms4UxFunGurYFoiR1SIF+iXRnXZ23oF8i7VnXtkDGirOFPZV7VUcuylhTZy7q/e5QxskGdh+OI+iJGTpAfsvN4ZdkqaMrv/Lbj1dP6nwKGcq7Q2FR9FXfFzwG/7n04WIldA6mTq2Bn3oW5bnFfiqMkL5+8u3z+IeO9cPpuYNi52gYSyVwjj51UIldUYAPVwkemykT8tgMn4gi7yzAaC7BSwvUF/K4TMnqEoZtZMpwOQa4xyhTwjDXV3lchr6pyR3+IWl1lzCQtCxJY5FWizuVU2uqyzHQEGgSBpLWJWkw0kJvgeWzWZ0ShpHWIofmqzdnZyiRQ/PVG41dXmu7swVexMsu/dMZSnEokDGZMIPebw4F+qW79A9kbLhUFrRFJsyYX7pMmLFI7smlf+DFVZkwg4zJhBlkrDgUyJhMmEHGZMIMMtadLeyp7MPZcnYRvk+XDmK/PtKFdo3CPDFSLD3X0U5yxHpTOrvAPyIJsxNVijQCTSinETJiXSiU1WDCDLIaSZgdS1uMSMLs1EEzsNiZg+YWS2mxh2oGE2bsxTB3mWpiUTZt4oyF2yzBjBZ0RTRhBn1hE2bQFzZhxrYY0ybMoMttwqwzsY9NppggTJIppsZgdgmDIm2PdZmVxRDYN5swg6RVCQNDwCbMIGldwkBrbMIMRlroLTBXrYl1ma2eZ/dYl9lcDYFQl1nalq2JnJuvPv1MByjUZHb1UWOaT6Ems30ZpTlbIGPd2cK0gUJNZnWZsekypkwGKtRkVlb9Emoyq6t+2d1tLspYdrlM5v1Qk1lb9kt1tkC/uBtdlDF3pYt6393poow5bRPo/ezk/iBj2ambQO9nJ6rbz7TbslP8o55wkn8wqnJ1KNDfMamTzpQFv2pXW1idSQvmgOzfeegExEz6mYRmiQn/QVZLTN8EsloC0n/9hIYcSHKecloCi515u8QUTOBDVVpsdfZiKFL/j8aB1DuhwRwUPIGuqEHFE+iLWH/Z8ns01l+2fCCrUvQEfv1j/WX7agDH+suWT36x/rLlQ1mVlzKpNfJSJvXNlMk/Zk3bZMaU+abJS5nwLdDkpUzom5Zl8g/CFJnKhKRVCQNDoEnSYEBH3gIpLcMMmZiFpE0Jw0Kgb5I0Zk2k1axfRcDOUCJpsyvKMkORKXOkF7eHWs22Vxg7RqnOFugXmTKHjMmUOfT+cLZAxqazhXlfyp9BxkL6Z2UZZXcokLHsGGPeHzJlzp6XIVPm0C9OC5z6RbaYQ7/IlDlkTKbMmfen0wOHjE2pycC8P50iOGXMSYJTW4qzBfpFJtChLcEEOtJU3WcPZKX3s8k2Qwi+fQmgrwXf/pQPuy3HU+X2q844LPnW89konWBKHfGct8C4yJ6Pf2hgSt2Zy/JmxtQdueyLQt9tPR5Wl7eYbjh7WHKsgy0te7MFk77QCtu/Cq0YEgZ9ivNm+1fR2zhbfTRoTbL9q8w3yV74zgzG9q9C39j+VQhj+1chabZ/FUaa7V+FkTZkYhH6xvavMtJ227/KrNmThGGRttv+VRYCe5b5S0hakdbAEKjSGuibyFsg5WXSQgn5fZm0IWFgpE2XwkbiojnSyXaNsjGU5NK+EEWm4yFjMh2PNJlzlul4yFh1yWVoS3PJZeiX7myBjA1ny8YYmy7ty/xSZAc780uRHezML0Wm45lfihtIQhlzE0koSnW2QMZkOh56X3aww+fFjauntrh59dD7ofGcc9X71Q0m6SfzF7IcyQn9LWdyUo5kAp5FVZUJeGhLcyjQL8FOdjSjINcRW31jq0da27ezQeaBQZ2nz1RwUidkNTiqE7IamdXZ0zENkdb2U04DY+vPvR3sZGcPVeux1dmLwQ7spHEgR9nDYI6O7oSu6Cm4PPNFtw3szBddjrGHG5luG9jZ97PLqUI0suTgTuqbLmGgb+ToTuobOVUI+mZsssjASBtJwjDSxi4LQJA0OVWIWlNkyQTC2AZ29niOJmFgpHVJGgyBIYsMEGZKGBYCc5OVGeabmSQMi7SQ4ltaPlOFFN/ScnJ2FlmZgaRVCQNDIFQ1W87PhhTg0vJHOqAAd11oapOhuKJZQ1LpZdtUcYbZUjZXNKMou0OBjGXHGERxsk8NzX0pm5N9on5xd1goY+4OC0Vxsk/UL072CfoluaJZQ+NySnJFM+iX5GSfKGNO9gl6P7k7LNQv7g4L9UtThSbqF1c0o4y5OyzUFlc0g37ZnexTO5nYVnYn9ASfkN0JPUF/7072iXrCyT5RW1zRjPoldmuloZFLZY8Vy9pgqwdkn9o4ewwCtbHTZyrH7qhAVnOsWAZZzQHZpzaPaQjIPp1zGqiNnXo7x2Sf4EOVY8Uy+GLIUvaJxoGsmtFgDso+QVeUYLUM+qJI2SfoiyKrZnAjU6TsE3R5kVUz+JkuUvaJkiarZtQaKftEfSOrZtSa6Soz0DdVVs2gNVVWzaBvqqyawZdNlbJP1BpZNaO+kVUzGmmyakZ9I2WfqG9k1Yz6Rso+Qd80WTWDvgmJv6Xlj3STVTPom5D4W1r+SDdZNaOkVVdnojCyakZJ667Q1BmKLJo1hjJdcYbZEpoxmpZRkrOFMdZl0QyiZFecgYzJohlEkUUzyJgsmkGU7oozaL5cCQm/lWW/yKIZY0wKv1GU5IozzC9DFs2YX4YsmkHGZNGsMcaqKzRBxmTRDNrSXaEJxpgsmkHvT1eqYX6Zsmh2MrW1TFk0Y/4OSb3tq/6eOVakQfPwygwMID6nPTaAmP7UJmTRvrj0K42tL/pat71ubw8B+7ouWmtn3IxA3aYfLxWYSXzms7rFZhKz4K1XfWrrumhHPvuiY/fss/z2EFCOKWaxWLccrFtA2oosKKDXb43JvK3uiWtsUOm+7BObgm8MRk5eoNZMCcN8k+S4YhhpyabgoTU2BQ+tydIaFgJW7g0GdLIpeEianLxAQ0BeXKG+keOKqW/kxRXom92m4JlvQnJvKS3DSLk3SppNwUOYIgsKkLQqYaA1TZIGrZEXV6g1Q8JAa+TNFTRMpkq5t1YYikzCQ1tkEh6iyJsrkLHibIEoMgkPGZNJeIgib65Axtz0FYri5N4gY1LujaLImyuMMSn3RlFkEh6NxaxFJuGhX5zcG2XMyb1RFHlzBTLm5N5aYd6XN1dYjEm5N+gXKfdGbXHib9D7Vd5jYd4Pib/9x3f/cF15cwX+eif3Rv0dvMGCBhLWoNxbK2z1yJWWk6nbNSL3dhohQbk3yGpQ7g2yGpF7ayc0RK60nHIakHs793bwBgt7qIJyb/DFYOXeaJRJuTcYblG5N+iKqNwb9IWVe4Pffiv3Bl1u5d7g19/KvdHIshdXIGm2agZJs1UzGGlS7g36xsq9Qd9YuTdImpV7gyFg5d6ob+S8cmpNlXUm6BtbNYPWdEkatEbOK6fW2IsrzJop55VDa6atmkFrdlmZgdZIuTdqjb24AmFs1QySZi+uQBhbNYOkyZsrmaHIohmaK9Ws3FtmKFLuDaK4GUmUMTcjiaIUVwKCjLkZSRTFzUiijLkZSRRFyr1BxuTNFYaS5M0VxlhI7q0so+yuOAMZczOSKIqbkUQZk0UziCJvrkDGZNEM2iJvrmSS02pW7o3ZYuXemC1W/I1534q/nQxFb1bubWccSbk3iCKLZtDfQbk3NGq1ReXedrZ6RO7tNHQitbF8slhU7o2xGpV7Y6yG5N7yMQ0RubczB4Xk3k4dFJR7Yw9VVO6NvRi03BuMMls1g+EWlXtjrgjLvTFfaLk39u3Xcm/M5Vrujblcy72xTUZM7m35TBaTeyvLpMkhSTTSbNUMRtqUdSbmm5jc2/LxT8u9Md9ouTcIk2VlBsJYuTfoG3vXDMLYqhkkrcs6E4Sxcm+QNHvXjFmj5d6YNTG5t+XPWrNVM0iarZpBGHvXDJJm5d6gNbZqBq359i3w+PH93dPxCeOldeTz6htbXRbLEkOZSzbsazZ0WSRjNnRZJIMo+xJTZZEpKesGbZCybhClLjHVFplqrvgCbeiu+AJRxhJTY5Gp6cohzIaQjFtbRkkrTM3Fd21Ivm0s25BdgQKiFJd8hyjVlQ7Q0OsWkW+7RjmZmt4igm3XSf2N/frhUCBHM5bcR0M629xiq29s9RTI9p85de6BxdLZYjmW3IesltjqkNUaKB2kYxpaINt/ymkPLHbq7RFL7rOHas7Y6ujF0LdN5vRRlPUtSZiNwezB3H5iZEUV16AvrOIa2mH0zd4dSQzGKq5Bl3dJGgxgO/QE+sYqrjGYmOLa6smlxxTXyjLMLpPtEMbeHYEwVnENhkCVpEEYmwWHpNm7IxDGKq5B0qYkjcHs9u4IhLF3R5hvtOIahMkSBpJm745Aa+zdEWiNVVyDMF1aA0mzimvQmilhmDVScq1OhpIcymAoa4nxtGiDuzVCbfj2yf90//Pl4ZeHD8//CxLwB9bc3jz99vFlxbv7j5+ebg5hawg2W9i25LEruAFOVFKEjXrMTUKh0edE2CCKFGGraCZqlyJsFU1b6wc9ciSkuwzpg545AtssbFkrdZ0+ScdcVlXAgU9SWXsbzMXYdjdMqA1DFT2oLW42CrTlqltufdzFF0u+Gp3wZWzC7ajt7SFgWh93UU/Ggfca6Fuv83ipLGZIHBHxysyPXlee5JeEyVroVDlxgcZOW7OiLVrR15Zf/fVjbfmx+Otn4BvxVZrnwA7wkThofEO43eKmJTrTtkZnqANuWz5eNNkHS2HWnv+0L5JVQzGQko2BFsPdLO7amyItvk7b2pviJYu8FAwyCwBhuswCoIkVvadQi1/tzIbg6b+x1Z3QOrXBtcXVxvzghNYpSnNnSTSnqstppzRy5Rn/ZCRb7/JUf7buQSscaeeDURqaZNpeiZ9Dzw6nB0FRcuzMyd4aoQmmc/WtEWqB21aftNEC56l+HJ6yak95GRKGveiGrNpDa+YWPFGxUJ2yWk9h5J01SlZeI+vqvdHBszDlXTX42ZlS4REGcEjb7fpgw14gU1bp4Rt9yrtqNMLm4pn2NMKOfDK2LXgKRI/h2OTdNEbSCM1CTXnxpTK2LE9J0JoiYVAAj5Ck21V4VWZMcyhICneEJN3SKyjHtgyHUpkt05Zmy3kC48Onp5MMxkibrc0GcZM7JjJWQ7JveRklu4MWe6ZCsm9lNdpDsm91GUUe3yFj3RZpg7E9bJU2iOtuwlU0s2Hs7iYcRUnucMsiZHc34qgt2aGwZ2qX6YDCbAncuqmHeaSxt2CZDfpWatjATcguu/epd6WGDfyUZalhQ2GShGG+ybJ7n8JkeZI+mYM0ss0EsNjKUrXm/Pfbsz/8/VKnBr7Gsz37Qxg53QG+yIvs0KcwNhcAYfZgpZR9S4rUp4GBvNhn91daZmerV3eQzQxlset2cfUekiehDI2QpAdd3am2Q4aqU22nKClWA2RM1bVqe1/87XI7DlH+/Sy/7JPv3zw+ffh42G3417rfHPken959/v83h+e9GtmLH4rnjquOuh/vfvm7DsSXG8jXv/qr9sOT1sNR7X4cxo7djyNNyVFtXY5FUVusy/U1sg5651Z7BXMoVdF23SwYBLZ7dUisnNJGYWwND0ah3cdDmMVuurRI1tDNicGYm7o7MQbcN7n5Zn7rSe6Okbr26FKLEoZJl1fxEkMpDmVjKNVWlbZAW+zowTMApM5NcqLUxZL41VIXqwMWCbvY07cY7CPZQkzMqOAxAhql7+LFjCru9AKNqw6FPWNXXX/8StaJ7tYYPXAaSsdLjWA3HCTXnh0Yu6s9fWPNipmCRxP46/fgtR746xd7+Obir4/es4G/vgZ3yvDXS00NCuP6d8pkKK5/pwyGMtWmhNkyQ+NY8yu27IcoSe5BDnD+/ss2Q/NZ6zKFrlmHhcPcitzxvEbh+Ylvbm5q47cctkOUphpNKIq7U09RhkOB8TDXNyfl8L74tAJ78DmJCewtPyhWYI/CZJvoLBHljBlT3OvLzpJ5QMpi7JrtNVCMxR7DHRZXVvwLkqyZSVb8Icy+2fxnjMU92fRnEFfmCymtWcKwR3x3CcOCLgXN3fUIlMZsaaEqPl29y6TntziN7L32oVraqYfkQQPdRpl5k9nP1zg8f2SzGwZPjZMHDXQjbWabHzywhoRhLu4I0Jh1LkFIPeXGw8MXRg5kDsvh5eOZ5URLyovMIBZ0d3OGegSvd6/slVbkREvo5iJvB1PSZIcBDIEie4Phc16q3nr3SDKoyJYDGhNd74l7KFFTht4Ut9DnITQMN+2r4Vll6wH0X3VD8UphKLtDqQwl231r6NrYrE4XiFpXHQr0VLP71iCH3abMg7hOO6ig6zqzOiUhiNI2mzOPcdic4hCMzLY7FPaUNdfbTG1xPQjUlkB7cznsDZixBsa6/ItlizOlf+hkdg1lONqMdRRA+ro9bjD6Qu2K1ztndCtwhtoVt7EMk3VOvkZSNb3IpDV0VpUw6NLd7LLjgVrTJQx8kEboHlnJbPXpdsOoDXcudiSWNRuGkx+hNjj5EYqSQ7fWKFNOdoTa4GRHKEoL3VqjTHW3w4M2DNd7AVGm2+ExlK/G7tId3uEFtrnajdgWf+kud3YshFa7EseiFbYbAVpR9f40dN9lzhbrGaX0+TaEoF1D7/GCwLYzAQXM5+ukMg0bMvBlEHCsUZeFzMvUWbnjowxm+YJKEMe+QihOlcUaiiOHiGIcqU+KcWzLEsWxbwaIk2wd4QDn7e3N3dPl15e77u8/XT4+3N2/rPL+3fNyz//uH+8eny6PT999un//4d3Pd/e/PP+3/708PH4+go9U+tx7y7PVUv744/8A1KowRA==

Если нужна гарантированная скорость выгрузки без простоев, например при строительстве завода по патерну главной шины Main Bus, можно соединить обе стороны выгрузки при помощи подземных конвейеров, соединяющих конечные манипуляторами с каждой стороны. Таким образом два манипулятора будут выгружать ресурсы на каждую полосу (lane) конвейера, кооперируя друг друга. Для гарантированного заполнения одной полосы экспресс-конвейера нужны три пакетных манипулятора, поэтому следует устанавливать две или больше железнодорожных станций Train stop в ряд, организовывая сквозную выгрузку. Также, для ускорения заезда следующего поезда на разгрузку можно поставить светофоры между каждым вагоном на станции разгрузки. Следующий чертёж позволяет организовать выгрузку 12 полных экспресс-конвейеров (правда есть вариант по лучше).

blueprint

0eNqtXdtuXDcS/BVjnqWAlyab9H/s08JYyPbAO1hZEnRZJDD87zsjO/FRRI6KVfsUO5a6T1/YJOvU6f62+3j9tL+7P9w87t5/233eP3y6P9w9Hm5vdu93Mb3b/353v394ePd4f3XzcHd7//ju4/768WF3sTt8ur152L3/57fdw+HLzdX16dcf/7jbH3/v8Lj/evyJm6uvp7/9FHH5l4jLk4jd96OIm8/733fv4/eLN4XcXx2uN7+Svn+42O1vHg+Ph/2Ph3j+yx//unn6+nF/f5T5128+HPUevvz78fJZxMXu7vbh8MO+b7ujpN79YvfH7v1l9f799CB/E5RQQTGE85Iy8Ug+EmTMIw0llbeCNHi28Fv5U6b9Vo4h+Xy433/68SM20FEJHfGMjjrQ4a90PB3z5P7L/e3xv1Mt6ZyWiz/z8Pbp8e7plK6vtLZNHK4+/efycPOwv388/stAVz6jKw1k9xeZf/lzdQwEl1+Cj38cBTmGzXPu99eXn/69fxg6xF4+5EhWXLC5LNocf621r/vPh6evl/vr48/fHz5d3t1e79944vKs4mZ/XA8fb5/uT1Uh1ouY44eRKmYxjj1iCx5pi3kdCxq6/nbo6rJ3+3nvpouUjw6uQwczS/JYryK0Jg83kyUZ8TV5VBZWw9FXpK8u+RQ4l6llLEWs1hxVvV1sUsIy9ijs7WqT8mLKvpQ6rgipXUSzUc4mWwnvanVLhdm2x36psJPfrgvJV6xerWCprYfwfNk51Rxrw/itLM+4uvgztzyjWNFyXD8/tY0HM3JGy0lTkiAHZkJJO6NkaIlpR1pMiXhuzpC7xINzHi/37JpYLNRNPZBnZifLnTuRJ6R+W1BtSoxNFjmbMmRTIq4GaZxYlglZkyQ1464ZmNGFE45lSSUuFnnoA+cuFtACtcYJhyqXdeLWMsmEEghZkwwtUb6TJGIHL4m8k0CRLJmUDoWymOyyzLisyFchagMplbzgQbWhuGwVtYWURloFldPSmRvfZInWwAib1I4ayfscFM2aSOmQV2tmbovDjaQac1uc+bQwwmbRruTVE6qMlb3YQpWxNvKyiT17ly+bzFblgTQKcplH2ShmM3Hmcuu/dAbkSuhZu0FHSIlpN2hMSdEswdxVNUsClG+uXdMjpKRpSjB3de3SDrmrBU1JHBf5Rl5gA7JNtqReyiP15i9zNkXIJlNtCpRNhbi/z2JeCVlhIsu56zqWP40TjgWyE1hAHPmgB+66Dq37HjnhUHnsibi/T7KqZ0LWJKu6frENxFmkF/K2jkWyktKxUOqvdCPjMvb2ChWA3uU7OVVtjyJIs6DSczw1y3ZFzi7qBXCcUVcyIy3MpLEveAPm80KKB0NaGUggjj3hzDV+GqXGSJtGqZP3dqhGxhhI8RETH8krNPj0Sb5DM/tWjJk0C/SayWZFyizmsvtr5daG3N5iZG679ZeWjmlxCed4rWUcqabZ0jAtXbMFi0sKEgoBxiVpDA4wLilptmBxSRrMhcZFI3GgcdFYHKjHNBrHsy1DuSrneZBXyPkucazn19rGDGCC9/wciCHHlyA+T/294WGtk5N/5srf6bMx14ucy5ignChkAvRzJvjPtY8dwxGgwbKWCQb0PIYKBXoYw2NWnEjmZhfZJkRz+dZ8bqHOTzaZZEKjcSGp0GB+msyFJsubMWToaQUy5jI8TV/L3P0S9bkpbOvR8vjxecCJrntcHn24PIxhRU8qkTG06Lm3ydfH4AIyiRg9LEbHAB5351zS2NMkOxq0p8j0aK7Olajd4Bw6KxbmdL1ZHBXTkjVbKhYp025woMeKdoMDPSberEEt4s3asbg07W4FaunaPRHLsRo0W7C41KjZgmVyTdo9EdSSNS1gXEy7jdbZt4VFk4vlbq3qnbdSh8Iq37Wd00vetSt03qvc1xKvbRlKd+byPUsvj4Qwnwkjb9aYVz1z0kGvGnFv97EbmJv1NECVEDYNEPflA1hEnPv0ASyw3uXrvlPfPQdZb6X0RhJmwNzZyG8nwFxomUQxsNXaTEYxuI2jFdIurMa1KtvFbcTNGTxlVrRaY6TNqlbrJDqD+bwHUjyWqj0yOMx4Z+mJRE6wRdszA/PMwtaZryOmKbXG71reXZYIXnG52nYnxYOBazJERO2NXf6YgtobU2AuwZsaCbVXSoG5BOczWoZtHELStBTMlqzBbKDHTIPZQFtEagkYl6p5rGBaRAAMtEWkloC2iNQSLPoxaLZgmRxFagnmsShSS0CPae1BUI+Z5jFQi0gtAT1WNS3Yqoxaw5A6azvEEMm2csHc7Sp0V6ieWkntFlK5Xl6J+9qqYi2sUuKkF0w60UFkml7JCGHTpmZcyxDUq5WTDnrVCchw4oZGoHzTABFdQqYBytwHUmAJzNwXUmCJyizGBT58lpFBpm9ZyvIXVudK7xm95CdWaLR07Iur7NlJTA8rQrnJdnE7Jc0kw8qfMR1FpkXLIiNtVrWMbCEChpTmi4GeZfpQT3YWY9qKzP1KEcGmMWeJYFhBsUaKx8o/TfvCnv7/QPuidpdCfmYFeq3In1lxmxfFANsohdpXJooBtin0GdNSNC0Ji1TVgEnQY65pAT3WNDAvYx7rmhbMYxQDrKx6rIrsTyzHGAbYFszD4sIwwLbAJOgx07SAHiuax8Ac07oIoXFxDTIE49I0W0CPdc0WLPoeNGAS85hHTQvmMaZ7WP/bjjyUmzW5WO662kuoUh0nkxcOKIQ6LyaXeaCZs8o5qzJmVSMQy2l6dULYpOdjaoEDKDG7GzdTBsyVlgj4M4/dQPQfmgaoGSFsGqDCAZRYOW+Vk46VqKZ/IMm0ukyN/UASdJpOBGWaXaY1nlhYjVaX+wqRO8oaqWx5S+lZtovbU7qRdmHFtRcGsJzVmV4ZabMSuEQ3C8uVf61x2PK21TsDfw53lhzInkRYLcohMnjoJGx5ocPX21tXDpk0HRuistTyK4ZlzxZSPPj0VYYhmb0xB5f1ZkovcQn2TZJBzXQzxQDbxA5qo5wpBlg8o2WYIRQDLK56jGKAhTNaxrZkDTAGtYjgNxj9ogHGYPRF8BuMvmuAMeixpkG5oC1d04LZQjUWs9VMphqL+bItWvt81JasAcbYekli6wMsx5jGYlsoF7SlalAuGH3XbAE9JrY+AHOsa4AxFpcsgt+Yx5ixkD2ueiyTfE+oX26mmGkvYFyq9XLeMNPwJnOT3rd5Qzcj+sLFcU+xbPGihGFjuJyJ3vo1zJ6ea66PBrgR2GscPyjDFp1ZbSRbFFs0FpUuc4OMOOXYc6tA68esGPbRypZkuJHpC5yNHD+H+lL/gpqrEcZ+QY2tjA1DbaHN3KwGGfVZ9HR1sLgZaHqX2szFceOz06rLJV2U6MP18WKOJIzWjWtRoeC0mbs3VDOmEdyoXhxdfOovV1Ic+4KF3LA1W1jIDRRfZGyKqnQM0WyDTZWGTZZ2TUvHtDQJNSodi5SGs4Eeo4hmYdVjVcPZUFu0r6xRLRrOhnpMw9lKw4akazgbmMkU0awsx8U1LaAtGskUjYtGMgVzjCGabbApVEuUUCNUi0YyBePiGskUzGRxUCWYyeKkSjQuGskU9ZhGMkWjrw2rROOi4Wygx8RxlWXS9zk3DVkDI9E4ZK1ArbwzOZ/y9bOPpauk0oGPkDt5K6rezuklELfSZunlhLBprnLjK9Es6px0LIt6WAcHy7Dxe+5xHRycBoiZWDkNUM8U0ggWkc6N3gDLeC8qpHhunc8v2uwUS9RpMt+0dMoskm+KRov8jBpbrRbkgRxc0bcQSbs6ZleS7eqcXcxky1mdsWCMtDaTRg6yRHOpkuLBkDoB9Y53Fgvkx9nYorXQCSR5GrYYGGmzlFoaZBlW9y7TB1lSZdhilvU2Si+JiqPuJImoYKJGEfyG5jlYFMFvx7Q0DTAGbekaYIxpSRrJFPQYRTQLy1qSBhiDHssaYAxqMU0L1FDXktZhAY2L1mIU1SKC36DHRPC7Ylo0kimYY1kEv0EtIviNeSyL4DeWY1kEv7Ecy1qLUTQuIvgNekwEv0EtGskUzTER/AajL4LfWPRNBL8n3fDNRPAbi4SR4Dc0ysBMpZUWajiFmXFWVcwqGfx2zioG/K6z9GLA72mukuA3mEUk+I1FszDg93DahhUG/J4FqDDg9yxAhQS/sSJSSPAbK+OF7CKKPnyVQWhmJIUVHfx2Si8LfoPRYsFvbLVWHfzmtpQqd1sgq34luy2AxbVS4PeszlQK/J6VwMqC32AuseA36FkK/B7vLJUFv7FFWynwe5YEToHfsyRwFvzGyr/r4DdVhj2TKDEWUTfZLGpXcxb8BqMlgt/QzBBzEfwumBYR/AZtEcFvTEsTwW/MY00Ev0EtIvMb1CIyv8G4iMxv0BaR+Q3aIoLfoC0i+A3aonVYKFBHcGsi8xuzpYvgN2ZLF8FvLPpd67CAekzrsFAM85gIfoNx0TosoLZoHRbQuIjgN5hjIvgNekwEvyFbShDB78nYiBKiCrFSE1BKIOFwaExH2RDN4G4HxWYuIqZqzf2ttE74mZGvPpQvoV94Ch+GCrlBW6ijiUFbZeIZYtDW3M1d6EcwcvMpcM8dKqIfXZ2Gro5ciwWs/pcYZRiTGc9RIjmqCzWLHEcPJmiUmymQBW5DTsO7HUxrUGSakE5Xx4ZzRrQjGFahH206Tp/fH5eHjZcH2WMBjTTTm3RSixIFrM3cnaLS7WBYjY4RPDVR8FSHrk7kNHpwzSYWUgPF65AaVekYatkWjYJGOJQkImsJ0+IaggPaIvZUAG0RkTXMliz2VMBsoahladkWEVkDtYjIGugxkVYKaikaggNqEXsqgFq03qVo9EVkDdSiTa4vUM/pYiKyhsXFRGQN85iJtFLQlqzhRKAWsadCwqIv0krBHBNppWD0XUOjQC0isgbGpWuYFxaXIiJrk5EBpcjIGjVcoxQSWYMmQJQiE00TZxVJNE2YVYWA+KaBZ9ijeSaMa1aK2k3SScFc6QQ4OBwWUmogwMGZTyvDHp1FuyYO9MNKYCXppFjpq0ZCe+DD680UmIkapepE00TpddKdYLTkafVk7a0s0xQrQh5I8VgVcp1Pym3EnhjMdlZnnKKPzkqgG4nFgj5n+aRgxlQG6h3vLO4M1Dv1a2OkTWPeSRgXq8+NnMAF1qsWZRiXKv8tkeg06DW9mQK1uzS2mQIYLRH8hkZrlCaC3wHT4hpgDNoi0kpBLWJDYcxjXaSVglqiBuViHutiTwXQFrGnAqhFpJWCHisalAvaItJKQVtE8Bu0RQS/QVu6BuVCWipDLdtqCZgWbXAXaotIKwVtyRqUC2oRwW/QYyL4Ddoi0kqhMVQ1iOB3wLSI4DcYFxH8nozeqFGEu7FIRBn8pkbYVKrD2gu9kdNLNh+OyH23RhL8Dph0BvyephcDfseZMBL8Br1Kgt+gVxnwezh7pyYG/J75NDHg9yzaiQS/sSKSSPAbK+MkyyxEqFZM7/E1sV0WQKfp4HegzGLBbzBajQSJsVowoJitgsTchpVZ8BurQlkHv7kNMVPg96xoZQr8nlWtzILfWC5lFvwGQ0qB3+OdJVPg99SvFPg9jTkLfmN10ljwG6tXFkm0FhTPYtygc3SMm9obTWd+U5vXgAH2cHd9eByfNU7vTZ6VGTS1pZoGelvHtPiSDWnRBg3sRm3QmN6glgHj65ynbM1TRWN4ozZoDG9US17yVF30lElQLWqDBm6jWuqSp9qip1yCaFEbmgSeolr6iqf6Yq2lJmO2VRuoyZjLFZ2ZjNmXay4zGbOfq7nDEwUzGXOrZTL/oVa1RahRI1oqxTF7obdzep2CAg2aUlJr46R3THpfxwZtMqqjeiCEzbJoofXZFgoE7fbEScdi9oIYBgKN1sdusHVscB6gQgibBqhSUCBYnNw56Q2TTvYBRR++q4CfMUNlaguy3kbpjaQ7sWg1eTgWWdkb2QgBLEJNboRA7pStkHZh5a8xnRGmRas5I21WtRrZ8QANaSfFY57Fh1VugMbJzoJOq3wBDU6j1BMjbRalnjkkEKzP3UjxWL0iJ1ZGtQz3Kuultp3uHPKJRquR4sFodQ0KhCZlOMPo2mpxTAvF8diCgq+teTsBfEDxOoe0xEWjsoZAggGipklvUULOdVr7UIO6fXtYg8LyYoCccl05l92I67QhWmheaEO0QC0xUC400YVRa39gUONq5xhgWxiTWlpxDSn3taQfdDE7J70vStc6i6JZRyFmrauB0TihqAs1Tijqwr7e1tImwwN8wypb70T50y2vWiR6Shfe44ehwkgAVT5+9iS0dxw9+8kbP7po2vjZM9HNb+56U/rvjZ8//WxNWef+L8x9bhKAqrS0G1tgp+6B4yfXxgQY1JTYmWZmWy0F0yK+4oaaIXrWvucCPZajeow1BlLyzO3x+Zx9wFYi9jtDQ6f1OwPTMItvxUEt2idfaBpqkwRQLeINAPSY1u/MoA6bbtwNoIoLyKJ6NjcCMnKxIxoYOVu7AWzOz4ZETJsxYIblhXgTALOvaodlMB7iwR/0WCMOteNToTENjCeyiogAQm3gnKG6bbVA3T68cLt9PGcNUDUWuW+bzEmIUaYd0EDXFe3EkrA0qNqJBdSifdiNprS4y0M9RLyIOB/UhcdrUKHSNF84Z47nA3YchIVheVDF3RzLA4YVtz2ogFrEXR1q7eJV3NWxWlO1T7xt0gTJKzFixPJYVGN22Iks8U0e9C2Ru7iPTz7VcY/qnvr6+YE91ZP2FQH0cYy7+A4P1GLcay7o8393cecGbajclxABs8HV90yR2n8G8z6hrxbAyIh7N+a7pjVlMehbQm9aUxawiDWtKQtqi9aUxSbfIXoz9b1VoLK4FVXvmRJ9Tq/WpxzNb/F2jq3VJr6WA235VRFOp4qby4fH27vhW7m/nv5VPjw8Xv34824YFJyLtzkEDb/59Q0V7+PhC/DeJmyf+tVbs9kbsw1H75xTTi/MeK9k5jw3cYt2Ic/Qxzbei8iZyo0qJlTvtXhO61CLS4eWDFH0vDfxrRPrwy7BHJh1LajknHPWTU/mLazd2dfSvoUkIhGkUZmizaBGcQeDphqlngtItRpoj/pUOxZgdaptyHwwjyZPyOgtEI2e8pAl3zbEPJxlMn2wGIndcfZkScIhMsRvaoskuj+pvdkx6eIOD7FfG0WmC2e0DHeJWLWd1jFbXORZDPQApYYh022NA5Otq8ZV5hjRUpDeMIDWpSihFGAapiTyCLJzPswikYDVaxIqg3q1SHgJmiEaXg8W3eTqIckZFKOlRnWZQH3XtWMK5rtMXPrzkK/ZMnUWmMgSzwIFMz5rWgzTYuJ7kGxUIcniKQH0YVWto2aft6wNH0ZjJx4TQC1d04JFyriWVKh0be4C6CmKZmdntAzPpNTg0bKsRdzoQY8V9fjEzDlv1CRSXzbONS0Ql7BRfenaGVvGWrp2VsKWKUPaa33VFoa015e3nqL1rgJzrBC9b/IYLXkxYBQ+IU1kabOUcsaMr1TTypww6c5hMeCzN6pZJfrs4p6N2UC1msvLWiJ3MsA8VZP6tiFT59+a1RcCpF6jqCGoN4t2agAzQty+QS1ONbREPdVUWICMf1dfnnB6PXBwBOZNF7d0LCNetLFDN9shebI58+J+Jsu0zTZixosXdlCL+Joe1CK+pge1NG17BLV07dKJaaHYeGVZi9YgA9WisfFQLRobD9Wi8edRLUUrr6CWSpTXIZepNWfK61HWh4vd4XH/9UQNu37a390fbk62XV8djTz+v388PF1dv3u6ub69+ny4+XL8l//u7x9+gCgtmvfkNfdazL5//x+qkFP9

Погрузка предметов

При погрузке предметов, чем больше промежуточных сундуков и манипуляторов, тем лучше. Старайтесь организовать загрузку с обоих сторон поезда, если это возможно. Важно равномерно распределить подачу ресурсов на каждый сундук с манипулятором, особенно на форпостах добычи ресурсов. Это позволит начинать загрузку вновь прибывшего поезда со всех сундуков, что может увеличить скорость погрузки. Следующие чертежи с комбинаторами распределяют загрузку промежуточных сундуков равномерно.

blueprint

0eNrlXd1u47wRfZWFru2v4o9EMhcf8F30okD3rnfFwnAcJRHgP0jyosEiD9D36JP1SUrZTuxIHGXm7AJF65vdjSMfjs5wSB7OkPsju18fqn1Tb7vs7kdWr3bbNrv7+4+srZ+2y3X/Wfeyr7K7rO6qTTbLtstN/1PXLLftftd08/tq3WWvs6zePlT/yO7U6+zTLzfLen31Ff36bZZV267u6urU+PGHl8X2sLmvmoj5/s02tls/PXfzI8Qs2+/a+K3dtm8qInlVzLKX7G5uw2tvxwBHf7BgfrYygWJ+e8NxvxUpJCO3yKVw7DvO47Lt5vW2rZou/iKBU77bFP8VyXuom2p1ekInkIt35E31UB8282odH2/q1Xy/W1epBtyHl45fr+J73e8OTe8Tr74lGimvaKiq9Xz1XLXdNPbJ+NjNtifr2/4Z1f/RVA/Xzq/jT67vGU9NVW2Hv1Gx07ymGHV8Rv0Eo0cTu2a3XtxXz8vv9a7pv7aqm9Wh7hbxdw/vWI9103aLUZf/Xjfd4di93ig6PjGvvlfNS/dcb5/6EGirHov/7b9kR/Y2+2Wz7Hqjsn//81/ZK5/Skqa0ICj1VNQnOA00p2UCOsjjKBmPKkcCyXICSSkEumBBa3n8FJL46V1KePvaG8dHDeF9ZeRGWpGRdirKP1ppqT6qLBL39nbivvcvHfgDlkuK5QJhubghljXNsh2w7CiSS2i8LdIrFeUgNMsZvZVgZtA53R+S2AHCtmkWdC5AUzIWtBJgW9nkozWEPWLYprCNALuQeU9fhuNDXOQ3T80u/s1AH7ESgd40xHZ/6JXGuLHLqNTu13WXHpD01eTMeAFBEGon7DCOZe/VNMXAlIRiEHaUAGGzuDCCwDTCIcQIAtMo2dLNaAibGJ6MkYSLyQccnwNkd+iICDGW0+N6K4ggTGEWAga0rMcZQfQZI8RmRZ8pJNFnBNFnrLAXBwib6GlWEm+lLJYtsE9jkkZqRHIZTtxag0BrFrSVCyUtEUqW3g6xwyW8p/ZHbCG30oispHcYrOWKTlsiQsPcjtCwBV9oWEppWGizTN8Qy/TWhB1uoHiyL2P7Z5o15AYI26QnhyKHNJcm0BSEZjjvXWhIz7E4LQyETXHKWnrpyyLGMCwULL20Fr59CWHzvOYgNcuz20NqlocdRGrWTrDCWKyXOaidDa2dJ1qTROnEiii11C41JKJZPilFkkk7jk/IHYbSChW7ZrwAb9ciSAaGsoRUKTGAlw5CIwbC0oMaFwuiALamkdZcztKUWtI/nII0sOEEptMQNiswnWwvQ3OGLzIwnRWKeQ7xhegF7E+NLK4EG9NIYw4S/6y53XkIm9elgDSxSmayoTSx4qh/r36i4CIfF1wUM+VdqubCA0ljJRHw3ggEPF00YBBtqW5HW3o6VRgF+5BmSsJ7CwnAnDNL+ALCVun535eQHMw5A4R3ELZiYXtIDvKwA4TN4iTkQuGpGJgKEocsLoKGsHlcGF6GkLI3FR3BgqIwR1aYoQBbU1BrJShBc2BVEpyosZJuTDMa86BsVMibBbCxiTejnaZyyfadl80FKldQEpgV+irXEDjTclbwX0lAxbHYQtqYSUcBgec8cCy3yrTcQeBMR3qh2Ms5FgcWqBX1DoVlWXkcKwWB83rHh5JUntQyyVp7pZBMqwm8klykbt54HrY8QXq2mlsjqOg8rtejlT9Zi6nk1fdnCtiGejrJOCoaVTaQliJ5xkRX+P8tG50o1I5yfDZ2C0G0R4j2t0T0xPkHNZLdhSaZhhKvY6qTg7CkWvUKPLBmUQ2lZceWp8E1BM60HErMjsHTnFsInElLIdPicUplWAxlarld0EHgTK69RI4fQZMwAUknMwmQFKZeBDAXXGFqPsEvRxhKilX1x/VSEg5MvU5ZT2poZSyiapk9UVLEqqUjraSKVQfhMtU4pHCa9qlHJCcZmgZMv56Z/bRTiMpYjdBvFsq8MqeCq9pWUXoUDH0LZmMTb8NqzmLpTGxosAWihJlDgy3lStiljyY6RK061jBgPYJd8rCDXGA62fHUieNyanRCtcjJY4m53NJSZqmaqLcNQ0sdKYULhSi0GzqffvQyeVB1tD3iFcm0Rph2N8R0v2FDMq34uw6Sgtkrucq6IEAVUIJ77MfkZCwqpM1p8LTlUMJ7TEvacgfJVSYtUMqb69AACauSWGmWmE5zFJxiSdOrCY/xyiWmv3h8lgYCJwnA5BbT1gIC58VbicktpuUOAmda7iEtx7Q8QOA8y10OyUae5Q46v8u1XCPHV7ngBlKQvNHZWchyJucFZDkTHJBUxKUWkKTiXcrjIEnFu0vIAZJKduOPnxAqcWk9XD6TksoDkkp27c9EAWQvoIaWRq+8LbqPH4weCMMHqDeDJNgtXWLjRMKAPGqsPCTBbulSJj8hdr36LAZo4jFFxro/QWElx4Z5oxCmyHhXCnlg/jFpgh1e7W9M6nrFmc7zb8mmLtPRsqm7503VxVZir7uvt8del2rr3FLqkEgqlC7Al2hqkXBarp6vAqm/TLRb9jeL9jVLu30Vw+RoRvan+NXTNrIo2qjQIgKon9xmmZ54go6gIGc9UKzr/xLrNu9LQn+W9z9+Pe99PTZrrr4uYudGrEojXWb9N4I+C6L3gFXMMHqs13F2I+7Ppej9eppEDr3D9CfX6E646B1DXd+rK/Ib3yuXef2hWtUPVcMcj3ImkWfUXxMWl3jIB7P170A0/PUEuX9ZHPlePDa7zeKUorrrmkMlmf37IwTD+Xw6bshiwKsTDjyXBGHf/iUu+QNZZX1NrrKgcQzyHDHIhaHvBou1MFq+Dd2tLu7m9o607y3o+/x/0PdIzH79pZ5PDZNTbjSfdRTNHXYL8WSo07XZ4cNWab2dt91un7wI/QzjRrUAqX7SVtG33W5xxMzuHpfrtpqdWlj0Lewrgev/duov3QmtXazrTX321xnz/Jlo7JZ5WiciMBrVvS2nklUJV+eZ2G5KFw5cHVbiXliviXvfVJCfodbEVaqXNdl9/cQQPu9oA9FDHHDWufweOR1lWhTSx/9m4O7qvzSYZetlVI/xsz8vm/XLl6cI+2W9Wz5Exf+lqdpoyapq42Pf47rttFb3yrqgXWlCWVj7+vofqk3vWQ==

blueprint

0eNrlXc1uI0cOfpVAZznbRdbvHBbIcYHNbW+LgSHbPTPC2pIhyUEGgR9g32OfbJ9kuyVnZHc3y+SnAMFOXyaZH7OqSVbVx69I1m+Lm/un9nG33hwWH35brG+3m/3iwz9/W+zXnzer+/7PDl8f28WHxfrQPiyWi83qof/dp9X+cHXYrTb7x+3ucHXT3h8Wz8vFenPX/rr44J6X70rYrdb3r36Enj8uF+3msD6s29MMjr/5er15erhpd53Mbz+578Zdf/5yuDqKWC4et/vup7abfqhOUnZhufjaT6KfxUAKvZKyuv3X1Xqzb3eH7m8mxLgfT4L4x9DN8269a29Pfx+Xi05Ph932/vqm/bL6Zb3d9T90u97dPq0P193f3X2T9Gm92x+uR7r4Zb07PK3uz+o4/Yur9pd29/XwZb353Otm3/ay9D/9t/6HbrcPj6vd6tBPavHff/9n8Xz8w83mNP19L8f1v+zau9eKXne/y70VPu/adjP8G3LPH5+nNMpVn5hQayOp1U9I96h00kgPb6U/da64+7zbdv8V5TtJfucUL9bZPh0en/rlMBovvvH+qxe7TozCr0aZkJMMXsyiF08Izq8Et+391e2Xdj+pBnojVeldJHtXELyrfJvQQ3u3fnq4au+7gXbr26vH7X1bm9nJQJu22ylutk+7fk9xvIzx48QorrFuLjw1WecMdomSXWhKMmkNkxDDuCBahkmwjGOzaZJsmrJMzaRlzBtAsfi7CwaLZdFi3+154OQly9KSdRE1GalMluybdn5/015vhD3bZePn0OsDbkpgQQWq9EMNAHHCfCAO+RrGWb718SL4ODlAyX5GSpYPFBromBpJx4Riv6DBfgQDV68S761QKpigVFPDUm817KOk4WCdozfN0YlzzEMn8NIUIwB1g2qfREC0V0nOVjQ5eU5QAdCk16BJbgDJQSXZWXGqyes51nDqW5cKYsBqxtImr+cKlh6eL04C18wohvLToINhHB0EgQhy9vNBziwjZzfcoFnaoDkCSg4zUrKrhSeD/YAlJScUj0tLA44YpMVbALQZ54M2vXwsdDhpAIYkuOmRuCnNSMly3NSFSW+VHEUlOxR0RxVbDIcMSSWeAciYNJDRm6OFZMEkXo4WfBzaToLiPgBfH1VfH61fH02IrMjbgx9uD+LXJyuoT5NiMgC9kwZ6eyRciBrJobECZpNzBhkphSFgjhIhE8yBh8mFevCgBfVB2vwCAWguzQfNBXmX6vT/VslJiu4CA0qOM1JyBTIPj4IghacBjibjNMINARWYBIERxeCSQHOU4CwAIMAxg6RR8y0DWeYbEbSc54OWo4yW/TAkydJeFmG0XDRwNhKe/lCg9AeYcs8anBLNIDpbMECsgOghjMzS5WhEQHRWrcgIp0qU6fv4JTmaupOPZihcJlWBQGGdIxQrGDQ5QpKP0DBc20VinVIDp08UIbOls9dkdktyACTK84FEUY4Pw/BWoSTJnoSnJRQgLSHBNwRFs5skGOFlIWUtoPipCAJhhKdTAMwKq3brlFF16MTD6E8wX25QgYL5MpJB0eOB2aTiyveIcYQgpUAtI/nO/f/MRstJzlEY39ZKqC7DwHbs0VNIPcNp0GNbTso3J4K8zFurZRkxxRF0lk7YjKSCTOwYU6KT+fud6ftlijMP7ykdS+FgzogCnEoBxVxdMVleUZDMkrGNpkB9QZKrx18/KdqcEWIzf5HvJwuPzC8lAxQ2z9K0SIu8FcbhBV+RDpwC40bdSi0wUXg02ZREJMdiwq++2yOyyJtX5zJD75UuaEpC1NzMSM3yFVOJ2tuPAtPIR1VPSYSz1aUF55oGjX1kkQ4W2Ugiz4dC++vjrt3vNTE9Dc7ddzlR11ixI7Hp3HSNR0M3WTcBFilacBDO7x/v14fp7YEs0NY15kDem7C5a8xrLhgHMC/BZEL/zpkXZDQd2s45+AuUA9jZN8q1cPf9devYPmSxbg7m8jfKRsWZV3IxDhDNauLGrCZ7TRg7hfnlojBzVRg3tl3bXCXGzjYANeoNl7/t3qSwOFkXO9tiVWcuDGIyqobhL9Dt6G+Kg9S03Iz6EDiS72TcqMDJiTmLjgKiaZqRpis59G6UHikSzY4iTFGSbs0keADWDQDRa7qaZSpmgtFWwF+panXjsqOYxKL+BlGCrtZeXxxGb7WrVkKouHLR8szuTYGYjgydbgfBjFCWpDqj2COydc0mOJiZRpu3cq5465DscEnsNMDRPFGbR1VSx92owqjIrTISzFoKHWAcZ4RPm1PrikohphtVrLhUROMVRNM0J03HiqaHpd5Fut9wvoFXidRqw1xvRM17C89cY0TNu7NkmL0URXpYpPjhOOmnwwfeQAGeoYdGcIJnLioj6+f6jU/0mrkWO60UahHi++xJaGCGVId+g7vgm8bRgYKeCQQTjjr4FS5h/xj6JK/3uCysjulPCRd8Cr1m6CqTjxcQdIwQdMN6jRq91Vg2E3OlBjvjaikAMafZWqKB8TPtr+Y6Bfa2kyESPIBO55ERmmhGXbNcrIRsoxwuakSQFyHq089J06mi6VG6kNg5ycUAE2aqDlcu4pSfqpmQi/a0PFOrHlep0hoTRsclIKja3DfVBdtEueITwyQcck6caEHovaDrywhRh14n2979eRq3J0JoM527Joju8zrZ3sx02TwsVfb3FEYeJlJyyc4d2tZsqlByyY/y0eSJwm1KndCmxyWc5guSSIjmm1ELqN7msj+UkeOKNF+CaD4/J01XCNWURytPPC3ttUSN7STKeDagcgCCB9Cdd+aCEmre25wyngaoVArODyqVgvCDKsEJIPOiRnC+gPgKEJmXC5yNqLNCaezfNABS739FwRMGVc1/XSE45VGpJoa/QBd9DSstTCmPAaHUCp4rqNtBSrzgkzy0XEq6gPz0Mo9bGxJPHZRQYsGTBXW9kpvmgixOr+KIqXEXcMQecGhq8ERCpdoYYFxVgj1MiCpnHuABdD2ym4jwgDPqt3lkcdQ8IHkJblODJ86pmm6SuQDiPEDSDVDwRkUuIucCOYjMUrXOImfPg0u2twEq+Rhx1Hpf7PJGr6oqrC2FXtT+pknNqUPNktl/nByNzRxfmp42lBqnarJJzk5v2WznLPQWiY12yUW4v9CU7U7doDrb5Wnb4cxX1K2ZDA+g22McRP/MqDsnOQv9Q2JKPlGDd0qq7eYyziM8C0y3oxPOBykHwPkg3foiPF9MOQDODilVFOEBlF+QAPopaQQjuWRZIxjngnQ65+YCfgsDZuxg4kb5TXjqmO6kMb/tcv4CHR43v/VCybYS+JKMsaSjAIkvIYMS5lvpgiGhk8n+VIgRN3G5gLhJQJ4i+eYCGichSjQnebMxwDWnfLPxcPQMpPxpTgBzGjgbD8VhUriK4dIcij7CBJRunzcnhZ8HUKomIwxXntMjkZUHoZs4YrjExzg98j6SK3PSNFeeQBnFblnkEs2lAmeqL6u22gC3PHdFNwCZyTdTc+gjESu+L+tG5BuLqmbzRIttopVncUZ9j6k4caIeoUpVTXgpIO3SXdbJjma+sUwrICF8Y1HxjSGb+UabF1QyS2nUZ5aKvDMgzw85VTt3iuYHiIxrtpIH3FlAnfxI9gcbim33MhdCnAfQ7b8ReT5nwpe/46O0sr+PCiG4ES9XTIUQWV4w36+mKw9u0PgCVMzspAi3nleeJBFuRa9d9vDjQ9oB8L6Ryn0FbkivRAoJblCvNHJyAP1bNILpAhK1IClIZH484sw7K63hL/imDJF3KVyQl1h0KUr2NyeSDemkBBT5Fo3gfAFlm5XaKReMURCuMTdAka9mTZozyNnZFkimC1jSjLCkGeAY+9eT3/8UD1CAKiPgOWhKI+Aco+7MyAkgpmhGz29Qpbl4T0MN0DSJ4WdGyFZq5qRpV9F00pOt5gKDbwwdqboRU4E5Rmp0A5jz78j0kMKRPxXphFHgIrYNo2LmKsnZJiqXmvf+Mlh9LE8UeRidVN1eqSD0IjU62cFKAZKbVkAE2C9SdaOlgtCL5HSyzfSibSkc+Q89s1bEXaeYn3S0LQVuKjxoGR1ELDWP5AZuYqbbHrmBOUbd9sgN8kw5zeiljiMLriamjp4l+ApCtpKbk6blO6p+axlo2jtR03B6o3ZVBpRA065KmGPUfgHMMWq/IKMPnZDwaAi/KgxB3mh5mfh7oTM7uEGeDuOw/X2MYByA4C8Q3oBhx/CcG92cPZonKc85wCKVeoYJQu0AQIpiqoW77xKrbC69oGz8poImQSoHACoOqAKaNEojOCdRh9yZ4JxE7QCMZ46iSvM4KVpzbnlnN1clsC3CZHNVApPRTAn+AulUJYhLm9GbGUcmRM2lsReDRcK5NNWbFsw4l6bqg8vs8NJcgtoVM9tZMVPT/yPLLFIBo6AjSIVuzBArpmpYyq9qPKyluS9qf1Pe+VLbufRN83FyODtRxtM6gYgypS8mM0dkcwxfodBLGTlGER0jw7W508Y7FlV3xuNp4xWYMdI5I964n1g3gEOIkhk9wXAkJEWiZERJRZGS8oQX5xLSqJvxxw+UZ6D9KQT5DJweAOd+lO4fYRUpvwC6p55RU+bjKS+tLxpdD4jNWBgqCqIwJ03LFzE9kh7uZCK29ji2VrWQY7wWhrxuAIfgR1V/Jw6EyPY62ebKFQo2HCYD9H6hDlwkiYdd8OaJettEK6fyKBFAvl/nYIff06F9gOC3qv01Q2Uw5HWy7ffUNpeKVLHUCNoncX8P9ntqm0tV6nU4GO6pI47ZddsjXguj3B4jdE89o9bYXClV4fE9tfi2K0NFQeTnpOnKPbUfJVJFWdN4rKI7m/FaGO0ASF9HmlFfR06Vo2b0lgdnkV6MUNAW56TpWigxOitjFDUNN7ikpDvK8FhF1cGEobdZSNXnghMUpiSdbDvXn2xwSm6V2bvPcDGKlG6yxzzRNtFKKJHGlxJizPPmIRldKJGmBQUE7qu6bHKCwpSok22/JbC5VHYVS412nRJES9ljHptLZbKEEkkMJRJ+v6DbHjMeq+i2xwzdL8yo+efR+pKv5NH2I+Zxc4aCtjgnTdeCtpGms5jympEnLWlGTZE413x6SCP6Pi3+968+3viKikdeuKQ8J8VXouXMelye4RcuSdV9hzP8wiVl3cFjfuGSiu2Mr4RAecRrFhE2muorWd5NJmUXsxKyTQnegp2zCHQKFEWpSoW5mF+4pDI9SeSFS+V6KGyGpDZ3rVTW8DixroT3Nmk3+gd++A8kWyOPCFDWqdH8iIDR4WtlMynpV32B38hU7n8FfjdAubcU5P1MmlE/q6P1JV8ZJbXpUVBB3lOgPCfFh4risxro+1cVp9ZUUG7G2YSVTELfmA8pdtNzPh9Sq9368OWhPXTT7dR5s94c1Tm1F74IVALls9yzl+wRN1ndfnnlIN0vnT9vDt1HdBPaPrad+Y/TWPyl+9FT2rLJiySXERyj36uXC6r8i7HrsOg6DCeiTrvOMYN46V2Ydh9vt3oRrE5/ktVz06+3S+3+0x9ud9/XQmqQjW/MySTM04LO6OB3/by3hH93Hm2xyKf1fXdk7I8fq1buz6et+ak3V+cm681d++sLFLQY6JsM900GHY2gtprBJmccdNferu/anW4zZKUeX4T+MWvivBiawRH4V2Ap/P0k8vHr9VHd159224frU7rwh8PuqTUcqb4vMR6ik+qicbJFstEi5U+wyE8Icvl5hFwQs/0Mmk2/UF4MN2nn9F6YV3Qw1b+qIDeZmf4PzdwDVOio+iMN7YeGWdaX8Ni08R3fyErTv3niUXcOhmlBZ1Tcy9lc7Q/bx0lK6CQljUpjpzxn33bWPmyvjyIXHz6t7vft8jTAdT/AY2twhn+cPOhwkra/vl8/rF/s9yLz5c9M+7bN8mnCLss+OHzBUYtJ3ZLZSGnaSGeo2//81ct3Vog7Lj8K9jZfoXOZFnRGYjfrzwrs/buwAe6WwjVn7nDvu3CtC0rXh/ahn9T9U/u4W296IuZ+ddN2brH4++rQ/vC5E/rD/XZ11wXPP+zafTeP237GXUS9P6Hz7HwqlCKXGLx/fv4fQR9A0w==

В предложенных чертежах производится расчёт среднего значения всех предметов в промежуточных сундуках и каждый манипулятор включается если в связанном с ним промежуточном сундуке предметов меньше чем среднее значение. Также, станция погрузки добываемых ресурсов устанавливает лимит на количество поездов, в зависимости от количества ресурсов в промежуточных сундуках.

Погрузка и разгрузка жидкостей

Чертеж разгрузки и погрузки жидкостей полностью одинаковый, отличается только направлением помпы. Приведу только один чертёж для одной вагон-цистерны и двух помп, его легко расширить на поезд из 4 вагон-цистерн.

blueprint

0eNqllmFvgyAQhv/LfZZGQBT9K0uz2Eo6MkWDuKxp/O9D2866XDbLvqmB5733uDu8wKEeVGe1cVBcQB9b00PxcoFen0xZT9/cuVNQgHaqgQhM2UxvttQ1jBFoU6lPKOgY/bmld60tT4q40rw/bGXjPgJlnHZaXaXnl/OrGZqDsp79QPCypzdHZvUIurb3u1ozSXpSlmcRnKEgIqbjFNAPEHsalOQ5BuLfoEZVemiIqtXRWX0kXVsrjJfsxJ2Y7oQ3b5TXP7SDnSzTdI+oJKtkk1t2EbhYwxGUCHCeYaD0G9Tpzh9lS062HUyFkeIlLDF7rrT1aZqXMISd4ZWCkNlCTnDDMsAwCspXhrH9fAmG4cHQeIEMTYce4R3Bt2SK0gB7HA2NhSQ93hQk3+6abgImAa7RQUBFUBnLfFOY6T+mw01iNR04Nhxo9nwyJDrMaECvSHQ40DyAhHYMWzpmAhnii/PXCpJ8fTC+VHpXXp8BMIWAFpJoCzH2/JyWFJ8UjAdEhd91Ac2S+frwd/F8axcP/wURfCjbXwteUr+MZSnPU5Ek4/gFc/anpg==

Зачастую, хватает и одной помпы на вагон-цистерну.

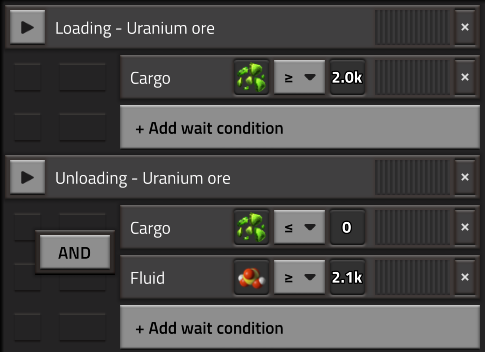
Погрузка и разгрузка урановой руды

Добыча урановой руды Uranium ore требует серную кислоту Sulfuric acid в количестве одной единицы кислоты на одну добываемую единицу урановой руды. Обычно используют состав поезда, где первый вагон-цестерна для перевозки кислоты к месту добычи, остальные грузовые вагоны для перевозки добытой урановой руды. Использование бочек с серной кислотой не столь эффективно: пруф. Одного грузового вагона урановой руды с одного уранового месторождения при использовании процесса обогащения Коварекса Kovarex enrichment process обычно хватает, чтобы удовлетворить все потребности в ядерном топливе, для этого нужно всегда возить к месту добычи не менее 2k кислоты. Поезду потребуется специальное расписание.

blueprint

0eNrNVFuO2yAU3Up0v/EIg7GN19Df+aqiiNjERcIQYcg0iryA7qPdWFdSIGmSzkMz89eviPs495x7j3OCrQ5y75Tx0J1A9dbM0H09waxGI3SK+eNeQgfKywkQGDGll7a9naxXBwkLAmUG+R26ckHvNgYnjApTYd19J1nWCKTxyit5np8fx40J01a6CP3aZAR7O8cWa9K4CMNp+8A4bRiCI3QFwzyOsE5FMHEuww8p2VttXepxKUI5KVnd1rxsKK44J3XDmrYksXDMHZi1LaENrpqSs4pWrME0p7cxjUCkooq3OAPFn7KqaU0iVt02bElLeaaGXNXsdFBD8STGSO6lnIq9K4ewV/DpFb8XbrRv4jPyoXUpc4gh62KRCVqnW839NzkEfTnW7SbpXd7lz176CwdfrBiUGVfF6vHsg1XyAYInofwmem/I9M6gEXIvnNxcbBQPhu4tFctDNG065qUtqdopN/vN5zyYPO9F+gAIxhhdBgufLAK/f/yCZVlnZ19lPBr9fwt5qeInZCM+4yLMcCOTvfgpNrnjRmcOehec6gvRx/C/my3f3Ow6+Snr6u7+jBBosZU6Lfu24NXVVggO0s2ZHWnLquGkqSmvWVUtyx9pL5Wh

Больше подробностей

Детальный разбор погрузки и разгрузки поездов смотрите на YouTube канале.